Blog 4: Design of Experiment (DOE)

dylanl21
Jan 13, 2023
8 min read

Updated: Jan 16, 2023

Case Study: Popcorn 🍿

This case study is about reducing the number of inedible un-popped kernels 🌽, aka ''bullets" to increase the popcorn yield 🍿. The purpose of this case study is to test our understanding of DOE and practice our use of the factorial design. Below are the factors identified, with their low ( - ) and high ( + ) levels.

Factors:

Diameter of bowls to contain the corn
Microwaving time
Power setting of microwave

Factor	-	+
Diameter / cm	10	15
Microwaving time / min	4	6
Power setting / %	75	100

According to the scenario, 8 runs were performed with 100 grams of corn used in every experiments and the measured variable is the amount of “bullets” formed in grams and the data collected is shown below:

Factor A: Diameter

Factor B: Microwaving time

Factor C: Power setting of microwave

Run Order	A	B	C	Bullets / g
1	+	-	-	3.46
2	-	+	-	2.46
3	-	-	+	0.74
4	+	+	-	1.46
5	+	-	+	0.95
6	+	+	+	0.32
7	-	+	+	0.46
8	-	-	-	3.12

Significance of Single Factors

Each of the highs and lows of each factor from the tabulated data are totaled and averaged out. The average highs and lows are used to plot the graph below. The graph helps to visualise the differences in the highs and lows of each factor and thus their significance through the difference in gradients shown.

When A (Diameter) increases from 10 to 15 cm, the average mass of bullets decreases from 1.695 to 1.5475 g.

When B (Microwaving Time) increases from 4 to 6 min, the average mass of bullets decreases from 2.0675 to 1.175 g.

When C (Power Setting) increases from 75 to 100%, the average mass of bullets decreases from 2.625 to 0.6175 g.

C (Power Setting) has the largest effect / significance, followed by B (Microwaving Time), then A (Diameter). A larger significance is equal to a larger effect on the variable, i.e. a larger change in the value of the measured variable per unit change in the factor. The steepness of the gradients and differences reflect as such and factor C has the largest gradient and difference between its high and low values.

Interaction Effects

A pair of factors are chosen and their data is analysed to help visualise their interaction with each other. When factor 1 and factor 2 is chosen, at scenarios where factor 2 has a low and high value, the data of factor 1 will be be tabulated for those scenarios to plot a graph accordingly. By comparing the gradients of the graph, we will know the significance of the interaction.

A x B

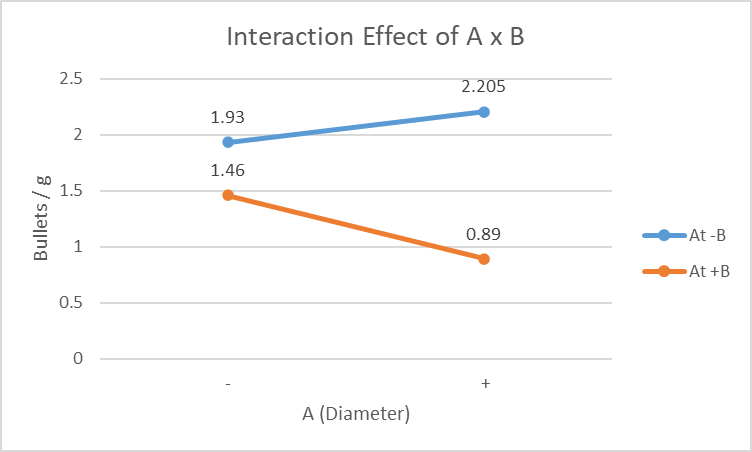
The gradient of both lines are different in that one is a positive gradient and the other is a negative gradient. Therefore, there is a significant interaction between A (Diameter) and B (Microwaving Time).

A x C

Although the gradient of both lines are different in that one is a positive gradient and the other is a negative gradient, the gradients of both lines differ less when compared to A x B. Therefore, there is a significant interaction between A (Diameter) and C (Power Setting) but not as much as A (Diameter) and B (Microwaving Time).

B x C

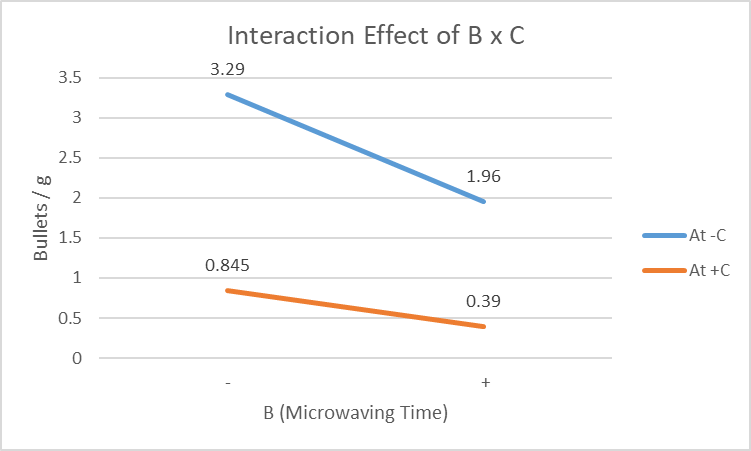
The gradients of both lines differ by a small margin. Therefore, the interaction between B (Microwaving Time) and C (Power Setting) is small.

Full Factorial: Conclusion

Power setting is the most significant factor, followed by microwaving time, then diameter which makes sense as the first 2 factors are related to the microwave itself which is needed for the popcorn to pop. The same reason is also why these 2 factors have a small interaction.

When diameter increases, the volume of the bowl increases so there will be more corn to pop. The larger amount of corn in the microwave can increase the number of popcorn and bullets. However, the amount of bullets decreased instead. This is surprising but its also possible that its because not every pack of microwaveable popcorn is the same as each other and what pops the popcorn at the end of the day is the microwave, that is why diameter is the least significant factor.

Fractional Factorial

4 out of the 8 runs were chosen to be analysed instead of the full 8 for the sake of efficiency. The runs chosen were 1, 2, 3 and 6. These runs were chosen as in this set of runs, all factors, both high and low occur the same number of times (orthogonal).

When A (Diameter) increases from 10 to 15 cm, the average mass of bullets increases from 1.6 to 1.89 g.

When B (Microwaving Time) increases from 4 to 6 min, the average mass of bullets decreases from 2.1 to 1.39 g.

When C (Power Setting) increases from 75 to 100%, the average mass of bullets decreases from 2.96 to 0.53 g.

C (Power Setting) has the largest effect / significance, followed by B (Microwaving Time), then A (Diameter).

Fractional Factorial: Conclusion

In terms of ranking significance, the results of the fractional factorial are the same as the full factorial which demonstrates the efficiency and resource-effectiveness of the method. However, the results also show its disadvantage in risking missing information. When using the fractional factorial method, the number of bullets increased when A increased, which is different from the full factorial method which showed a decrease instead. This also helps to support my conclusion about the diameter and its effect on the bullets.

Case Study Spreadsheet: https://docs.google.com/spreadsheets/d/19U2qywgoK-VbZZvUNmYrdBjIwn7pfBgl373BJ7bl458/edit#gid=0

Practical

For our CPDD practical, we were to practice using DOE on a small toy catapult. Our group would be split into 2 smaller groups. One would do the full factorial method and the other would do the fractional factorial method. I was in the group doing the full factorial method, with my group members, Darel and Kerri. Afterwards, we would do a group challenge.

Factors:

Arm length
Projectile Weight
Stop angle

Factors	-	+
Arm length / cm	28	33
Projectile weight / g	0.8619	2.0117
Stop angle / °	10	40

A tray of sand was also used to help see where the projectile would land as it would make a dent. We had to flatten the sand every few runs as the bumps produced by each run may make the following runs less consistent. The sand also made me sneeze so I wore my mask 🤧

For the sake of efficiency, we also counted the number of clicks the gear of the catapult would make when pulling it down so that we would not have to check the stop angle every time. We also flattened the sand with the protractor when there were too many dents in the sand and it would make the results too inconsistent.

After we did 2 runs of 8 reps, the rubber bands of our catapult fell off while I was trying to change the arm. While trying to put it back, one of the rubber bands broke. We got a new rubber band and fixed the catapult, but now we had to redo those 2 runs because of the different tension of the new rubber band. 😩😩

Below are our tabulated data and results,

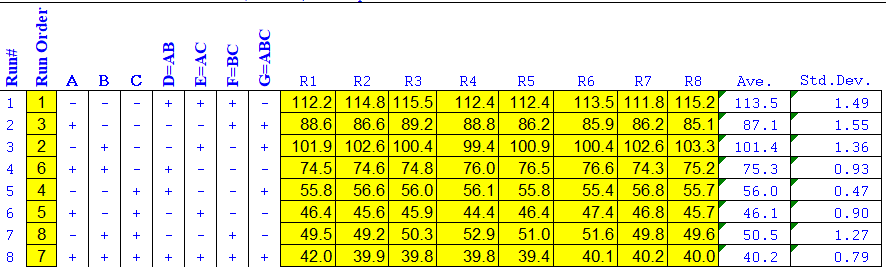
When A (Arm Length) increases from 28 to 33 cm, the average distance travelled by the projectile decreases from 80.36 to 62.15 cm.

When B (Projectile Weight) increases from 0.8619 to 2.0117 g, the average distance travelled by the projectile decreases from 75.66 to 66.85 cm.

When C (Stop Angle) increases from 10° to 40°, the average distance travelled by the projectile decreases from 94.33 to 48.18 cm.

Stop angle is the most significant factor, followed by arm length, then projectile weight.

Group Challenge

The group challenge was a table with 4 targets with the image of our lecturers on a table and we had to use our catapults from a designated area to hit them. The groups would be ranked according to the number of targets hit and will receive marks based on the rankings.

Each group was allowed 3 trial shots and 2 actual attempts per target. For the first target, we spent a few minutes as I was using the measuring tape to measure the distance between the catapult and target and looking through the data to find the appropriate levels to use for each factor. My group member Darel was manning the catapult. We used 2 trial runs for the first target and 1 actual attempt on the first target to land a hit. The first trial shot was a miss so for the second trial run, I chose a run we did with less distance travelled and the shot landed so we proceeded to land our actual attempt afterwards.

On the second target, we used our last trial run and both attempts but we failed because our projectile would bounce on the table first, then go over the target.

We hit the remaining 2 targets that were much more difficult though :V

The third target was considered difficult because it was behind a covered electrical socket and thus, the catapult had to be angled to shoot it. The distance from the target meant that the angle we used for the catapult would have a larger margin of error. The last target was difficult as it was the furthest away so it was the hardest to aim straight at. I used a measuring tape while my group member Kelvin used his sight to see if the catapult was aiming straight at the target from the other side of the table. For the last 2 targets, we used the levels of run 3 but not exactly. Darel would adjust the stop angle of the catapult according to his gut. Because both targets are more than 100 cm away, the projectile would be less likely to bounce over them due to the angle of their curved path.

My group ended up ranking first among the groups 🏆🎉🎉

Thoughts

In the tutorial, I was initially confused and intimidated by DOE. I was intimidated by the amount of numbers in the slides shown and confused by the interaction graphs. After doing the pre-prac, I was more familiar with doing DOE and realised it was not as difficult as I thought after plotting out the graph. However, I still felt that I did not fully understand the DOE process completely.

After experiencing using DOE in a practical, I found the process very repetitive and boring as we had to do a lot of reps. The tray of sand used cannot be flattened consistently the same way and the shape of the sand would affect the results. The catapult would also be inconsistent with the distance of the projectiles by a large margin sometimes for an unknown reason. This made me realise a weakness of DOE.

For the group challenge, the data helped but only to an extent as unlike the sand pit, the table was hard and would make the projectile bounce. The distance travelled by the projectile would also still vary with the same level used for each factor so a bit of luck was also involved. This experience once again, helped me realise a disadvantage of DOE.

After comparing the results of the full factorial method and fractional factorial method, I realised that the rankings of significance of the factors are completely opposite to each other. I think that this may be because the tension of the rubber band can affect the other factors in a significant way and that it would be able to change the significance of the selected factors.

The case study, unlike the pre-prac, required me to find out the interactions between the factors. After typing out the data for the interactions and plotting the graph, I once again found the process repetitive and time consuming, making me feel bored.

The tutorial, practical and case study still helped me see the advantages and disadvantages of DOE and reinforced my understanding and use of it through repetition.

Advantages:

Helps in designing an experiment for easy visualisation and analysis of data.
Helps to understand which factors affect the dependent variable more.

Disadvantages:

Time consuming, depending on the amount of repetitions, even with fractional factorial method.
When doing experiments, there are other factors outside of the selected that are difficult to control or maintain, which may affect the consistency of the results.
Analysing the data may require looking beyond the data and the context of the data.
Results may not be used properly if certain factors were not considered.

These are my thoughts on DOE. My opinions on its advantages and disadvantages may not be correct or lacking, but my view of it may change if I use it more. I hope I would be able to put what I learnt to use when creating the prototype with my group.

Comments